Harmonic Number Games
Mark Pottenger
The basic physical definition of a “harmonic” is an oscillation whose frequency is an integral multiple of a fundamental frequency. As used in astrology, the fundamental cycle is a full 360° circle. The term harmonic has come into astrology through the statistical work of John Addey in England. (The word is also used by John Nelson, but he uses it to refer to a series of aspects—something entirely different from the subject of this article.) Distribution of zodiacal positions in a sample can be graphed and analyzed like the physical waves to which harmonic terminology best applies. If there is only one peak, it is the fundamental cycle of 360°—which can also be called the first harmonic. Two peaks show the second harmonic, three the third, etc. (Assuming the distribution is even-looking like a sine wave. Uneven intervals between peaks show combinations of harmonics.) The basic nature of harmonics is that they complete some whole number of cycles in the interval of the fundamental cycle being completed once.
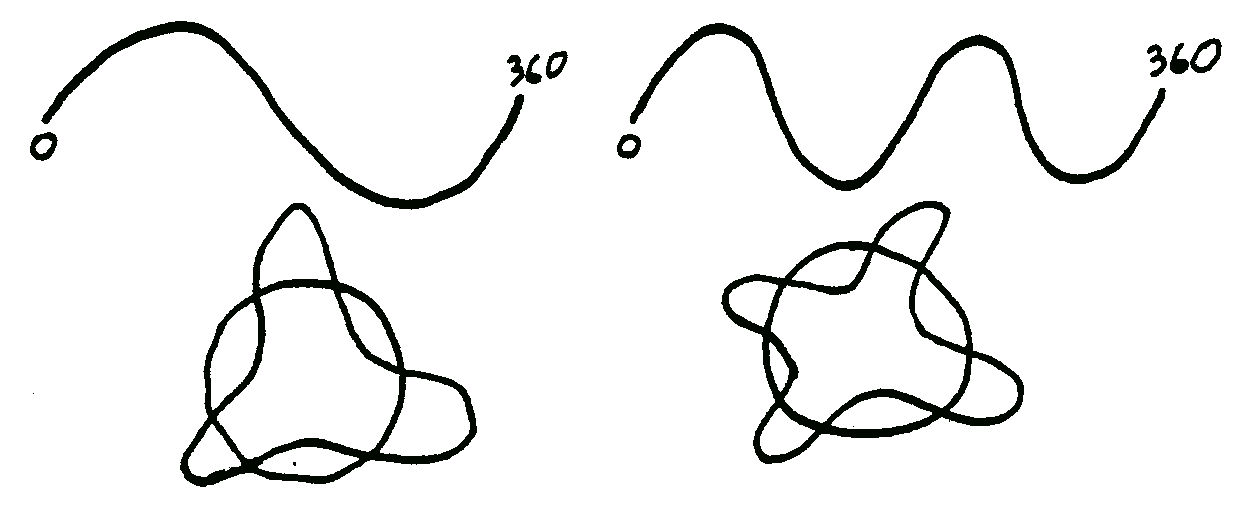
As you can see from the drawings, harmonics can be presented in either linear or circular graphs. The harmonic number can be viewed either as the number of peaks (or troughs) or as the number of repetitions of the cycle. Cycle length is the inverse of harmonic number—the larger the harmonic number, the shorter the cycle, to fit more repetitions into the fundamental length.
Note: for the rest of the article I will give zodiacal positions in absolute longitude (up to 360°) rather than in terms of degree, sign and minute.
The basic phenomenon of cyclic repetition is used in a variety of ways in astrology. One method is to chop up your original 360° into equal segments and superimpose them. This is the approach of the German “dials” and American “sorts”. Whatever harmonic you are working with, determine the degree measure of one cycle. (E.g. 4th harmonic = 360°/4 = 90°.) Positions up to one harmonic cycle are left alone. Positions above the full cycle length are brought down into the desired range. This can be done either by subtracting the cycle length or starting to count from zero at the end of the cycle—the actions are really equivalent. Whenever you complete a cycle, you start counting from zero again or subtract another cycle length. When you finish, all your positions will be between zero and the length of one cycle in that harmonic. The resulting sort is an excellent tool for spotting aspects. Anything separated in the original 360° chart by the length of the harmonic cycle will be conjunct in the sort. Thus, in a 72° (5th harmonic) sort, all natal quintiles and biquintiles are conjunct.
If one does a lot of sorts (especially those with all midpoints) by hand, it helps to have a table giving the degree and minute at which each cycle ends (the amount to subtract from positions above that point). For example, the fifth harmonic completes cycles at 72°, 144°, 216°, 288° and 360°. To get the sort, positions less than 72° are left alone, positions from 72° to 144° have 72° subtracted, from 144° to 216° have 144° subtracted, and so on.
Sort positions can also be gotten with a calculator. Convert the natal longitude (L) to decimal if it is degree and minute. Divide 360° by the harmonic number to get the exact harmonic cycle length (360°/H=C). Divide the longitude by the cycle length (L/C=Q). Subtract out the integer (whole number) portion of the quotient (Q-int[Q]=R). [Note: int(x) means “the integer portion of x”.] Multiply the remainder by the cycle length (R*C=S). The answer is the sort position.
If your calculator doesn’t have a memory to store the cycle length after calculating it, an alternate approach eliminates the need. Multiply natal longitude by harmonic number (L*H=A). Divide the answer by 360 (A/360=Q). Subtract out the integer portion of the answer (Q-int[Q]=R). Divide the remainder by the harmonic number (R/H=B). Multiply this answer by 360 (B*360=S). The answer is the sort position.
The crucial part in both sequences above is subtracting out the integer portion of the quotient (Q). This is what gets rid of extra harmonic cycles and brings the position into the proper range. The rest of the operations are first to get that integer, then to undo the changes and get back to degrees.
To summarize the three methods of doing harmonic sorts. By hand: Longitude - nearest value below in table of cycle ends = sort position (L-TV=S). Calculator with memory: 360/Harmonic number = Cycle length (store) (360/H=C). L/C= Quotient (Q). Q - int(Q) = Remainder (R). R*C=S. Calculator without memory: L*H= Answer (A). A/360=Q. Q-int(Q)=R. R/H= Answer (B). B*360=S.
As you can see from the summary, using a table is the easiest way. A quick example: Richard Nixon’s 72° (5th harmonic) sort positions for Vesta and the south node of the Moon (by table): Vesta (19 Sag 0) 259° - 216° = 43°. South Node (7 Lib 15) 187° 15’ - 144° = 43° 15’.
A natal quintile shows up as a 5th harmonic conjunction.
In addition to harmonic sorts, there is another whole approach to harmonics suggested by Addey. You overlay the positions, then you expand your sort to again fill 360°. Thus, your harmonic sort becomes a harmonic chart that you can read just like any other chart. If you have already done a harmonic sort, you get longitudes for a harmonic chart by multiplying sort positions by your harmonic number. (S*H=HL) (E.g. Nixon’s Vesta: 43° * 5 = 215° = 5 Scorpio.)
If you haven’t already done a sort, you can get harmonic longitudes directly without sorting. Multiply the natal longitude by the harmonic number to get the harmonic longitude (L*H=HL). If the HL is less than 360°, that is the final answer. If it is greater than 360°, subtract 360° (repeatedly, if necessary) so it will be less than 360°. If you are doing this by hand, a table of multiples of 360° is helpful. On a calculator a technique like that used in the sorts brings the answer into the proper range. HL/360= Temporary (T). T-int(T)= Remainder (R). R*360=HL. (E.g. Nixon’s South Node: 187.25*5 = 936.25 - 720 = 216.25 = 6 Scorpio 15.)
How to read the harmonic chart produced by these procedures is still very much a question.
Harmonic Cycle Starts/Ends & 360 Multiples
|
Harmonic 2 |
Harmonic 3 |
Harmonic 4 |
|
0 0 |
0 0 |
0 0 |
|
180 0 |
120 0 |
90 0 |
|
360 0 |
240 0 |
180 0 |
|
|
360 0 |
270 0 |
|
|
|
360 0 |
|
Harmonic 5 |
Harmonic 6 |
Harmonic 7 |
|
0 0 |
0 0 |
0 0 |
|
72 0 |
60 0 |
51 26 |
|
144 0 |
120 0 |
102 51 |
|
216 0 |
180 0 |
154 17 |
|
288 0 |
240 0 |
205 43 |
|
360 0 |
300 0 |
257 9 |
|
|
360 0 |
308 34 |
|
|
|
360 0 |
|
Harmonic 8 |
Harmonic 9 |
Harmonic 10 |
|
0 0 |
0 0 |
0 0 |
|
45 0 |
40 0 |
36 0 |
|
90 0 |
80 0 |
72 0 |
|
135 0 |
120 0 |
108 0 |
|
180 0 |
160 0 |
144 0 |
|
225 0 |
200 0 |
180 0 |
|
270 0 |
240 0 |
216 0 |
|
315 0 |
280 0 |
252 0 |
|
360 0 |
320 0 |
288 0 |
|
|
360 0 |
324 0 |
|
|
|
360 0 |
|
Harmonic 11 |
Harmonic 12 |
Harmonic 13 |
|
0 0 |
0 0 |
0 0 |
|
32 44 |
30 0 |
27 42 |
|
65 27 |
60 0 |
55 23 |
|
98 11 |
90 0 |
83 5 |
|
130 55 |
120 0 |
110 46 |
|
163 38 |
150 0 |
138 28 |
|
196 22 |
180 0 |
166 9 |
|
229 5 |
210 0 |
193 51 |
|
261 49 |
240 0 |
221 32 |
|
294 33 |
270 0 |
249 14 |
|
327 16 |
300 0 |
276 55 |
|
360 0 |
330 0 |
304 37 |
|
|
360 0 |
332 18 |
|
|
|
360 0 |
|
Harmonic 14 |
Harmonic 15 |
Harmonic 16 |
|
0 0 |
0 0 |
0 0 |
|
25 43 |
24 0 |
22 30 |
|
51 26 |
48 0 |
45 0 |
|
77 9 |
72 0 |
67 30 |
|
102 51 |
96 0 |
90 0 |
|
128 34 |
120 0 |
112 30 |
|
154 17 |
144 0 |
135 0 |
|
180 0 |
168 0 |
157 30 |
|
205 43 |
192 0 |
180 0 |
|
231 26 |
216 0 |
202 30 |
|
257 9 |
240 0 |
225 0 |
|
282 51 |
264 0 |
247 30 |
|
308 34 |
288 0 |
270 0 |
|
334 17 |
312 0 |
292 30 |
|
360 0 |
336 0 |
315 0 |
|
|
360 0 |
337 30 |
|
|
|
360 0 |
|
Harmonic 17 |
Harmonic 18 |
Harmonic 19 |
|
0 0 |
0 0 |
0 0 |
|
21 11 |
20 0 |
18 57 |
|
42 21 |
40 0 |
37 54 |
|
63 32 |
60 0 |
56 51 |
|
84 42 |
80 0 |
75 47 |
|
105 53 |
100 0 |
94 44 |
|
127 4 |
120 0 |
113 41 |
|
148 14 |
140 0 |
132 38 |
|
169 25 |
160 0 |
151 35 |
|
190 35 |
180 0 |
170 32 |
|
211 46 |
200 0 |
189 28 |
|
232 56 |
220 0 |
208 25 |
|
254 7 |
240 0 |
227 22 |
|
275 18 |
260 0 |
246 19 |
|
296 28 |
280 0 |
265 16 |
|
317 39 |
300 0 |
284 13 |
|
338 49 |
320 0 |
303 9 |
|
360 0 |
340 0 |
322 6 |
|
|
360 0 |
341 3 |
|
|
|
360 0 |
|
Harmonic 20 |
Harmonic 21 |
Harmonic 22 |
|
0 0 |
0 0 |
0 0 |
|
18 0 |
17 9 |
16 22 |
|
36 0 |
34 17 |
32 44 |
|
54 0 |
51 26 |
49 5 |
|
72 0 |
68 34 |
65 27 |
|
90 0 |
85 43 |
81 49 |
|
108 0 |
102 51 |
98 11 |
|
126 0 |
120 0 |
114 33 |
|
144 0 |
137 9 |
130 55 |
|
162 0 |
154 17 |
147 16 |
|
180 0 |
171 26 |
163 38 |
|
198 0 |
188 34 |
180 0 |
|
216 0 |
205 43 |
196 22 |
|
234 0 |
222 51 |
212 44 |
|
252 0 |
240 0 |
229 5 |
|
270 0 |
257 9 |
245 27 |
|
288 0 |
274 17 |
261 49 |
|
306 0 |
291 26 |
278 11 |
|
324 0 |
308 34 |
294 33 |
|
342 0 |
325 43 |
310 55 |
|
360 0 |
342 51 |
327 16 |
|
|
360 0 |
343 38 |
|
|
|
360 0 |
|
Harmonic 23 |
Harmonic 24 |
Harmonic 25 |
|
0 0 |
0 0 |
0 0 |
|
15 39 |
15 0 |
14 24 |
|
31 18 |
30 0 |
28 48 |
|
46 57 |
45 0 |
43 12 |
|
62 37 |
60 0 |
57 36 |
|
78 16 |
75 0 |
72 0 |
|
93 55 |
90 0 |
86 24 |
|
109 34 |
105 0 |
100 48 |
|
125 13 |
120 0 |
115 12 |
|
140 52 |
135 0 |
129 36 |
|
156 31 |
150 0 |
144 0 |
|
172 10 |
165 0 |
158 24 |
|
187 50 |
180 0 |
172 48 |
|
203 29 |
195 0 |
187 12 |
|
219 8 |
210 0 |
201 36 |
|
234 47 |
225 0 |
216 0 |
|
250 26 |
240 0 |
230 24 |
|
266 5 |
255 0 |
244 48 |
|
281 44 |
270 0 |
259 12 |
|
297 23 |
285 0 |
273 36 |
|
313 3 |
300 0 |
288 0 |
|
328 42 |
315 0 |
302 24 |
|
344 21 |
330 0 |
316 48 |
|
360 0 |
345 0 |
331 12 |
|
|
360 0 |
345 36 |
|
|
|
360 0 |
|
Multiples of 360 |
|
360 |
|
720 |
|
1080 |
|
1440 |
|
1800 |
|
2160 |
|
2520 |
|
2880 |
|
3240 |
|
3600 |
|
3960 |
|
4320 |
|
4680 |
|
5040 |
|
5400 |
|
5760 |
|
6120 |
|
6480 |
|
6840 |
|
7200 |
|
7560 |
|
7920 |
|
8280 |
|
8640 |
|
9000 |
A note on language: All of the math in this article works just as well for numbers that are not integers as for those that are. However, the results should not really be called harmonics when using non-integers. Harmonics, by definition, involve integer relationships to the fundamental cycle—a whole number of smaller cycles completed for each main cycle. Thus while the math of harmonics produces results with non-integers, we need a new name for those results. I have been using the term “expansion factor”, but it is awkward and I would welcome a better term. One form of non-integer “harmonic” now being tested is using the solar arc for an event as a “harmonic” number. Natal positions are multiplied by the solar arc instead of having it added. Opening up the area of non-integer “harmonics” increases the problem of proliferation of charts. True harmonics have already added dozens of new charts. Expansion factors can create an infinite number of new charts.
When doing a series of Addey-type harmonic charts for a single individual, it can be seen that positions change systematically from one harmonic to the next. I will describe the behavior of the numbers without offering any interpretations as to meanings.
When you increase the harmonic number by one, the harmonic position moves forward in the zodiac by the amount of the natal absolute longitude. For a natal (1st harmonic) position of 30°, the 2nd harmonic position is 60°, the 3rd is 90°, the 4th 120° and so on. This change from one harmonic to the next is really just breaking the multiplication that produces harmonics into successive additions.
As long as the natal longitude is between 0° and 180°, this addition will appear as increasing longitude with successive harmonics. However, if the natal longitude is between 180° and 360°, successive harmonic positions will show decreasing longitude. For example, a natal 330° becomes a 2nd harmonic 300° (660°), a 3rd harmonic 270° (990°) and so on. The numbers in parentheses are the raw answers from multiplying by the harmonic number (before subtracting extra sets of 360°)—you can see that those do increase. The harmonic positions decrease because the true increase each time is most of, but not quite all of, a full circle. The amount of apparent decrease is the distance the natal position falls short of the end of the zodiac.
The nearer a natal position is to the start or end of the zodiac, the less it will change from one harmonic to the next. Positions in the middle change the most. For example, a natal 180° becomes a 2nd harmonic 0°, a 3rd harmonic 180°, a 4th harmonic 0° and so on. It flips clear across the zodiac every time. In contrast, 0° stays 0° in every harmonic.
To summarize the apparent motions from one harmonic to the next: Longitudes less than 180° add the natal longitude each time. Longitudes greater than 180° subtract the natal distance short of 360° each time. Longitudes near 0° or 360° change slowly. Longitudes near 180° change rapidly.
The following short lists show natal (1st harmonic) through 5th harmonic positions starting from different parts of the zodiac: 1, 2, 3, 4, 5. 90, 180, 270, 360 (0), 90. 179, 358, 177, 356, 175. 181, 2, 183, 4, 185. 270, 180, 90, 0, 270. 359, 358, 357, 356, 355.
For non-integer expansion factors the position will change by the fraction of the natal longitude that your factor changes by. Increasing the factor by 0.1 will add 0.1 of the natal longitude to the expanded position. E.g. 30°*2.1 = 63°; 30°*2.2 = 66°. Because so many different decimal fractions are possible between any two integers, expansion factors can jump around quite dramatically between successive integer harmonics. For example, Nixon’s Sun for harmonics of 61, 62 and 63 is at 13 Aries 32, 2 Aquarius 57 and 22 Scorpio 21, while the solar arc of 62.229 for his resignation produces an expansion factor Sun of 9 Aries 12. The integer harmonic positions move evenly backward, while the expansion factor position jumps.
The angles between factors also change systematically between successive integer harmonics. Angular separations increase each time by the natal separation, just as positions increase by the natal longitude (in fact, because of the position changes). A natal separation of 1° becomes, in successive harmonics, 2°, 3°, 4°, etc. A natal conjunction stays a conjunction, but with an increasing orb. As with positions, natal separations near 0° change slowly, and those near 180° jump around.
If the natal separation is exactly 180° (an opposition), as in any angle axis or the Moon’s nodes, successive harmonics will be conjunct and opposite. On all even numbered harmonics, natal opposition axes become conjunctions. On all odd numbered harmonics, natal opposition axes are again oppositions. E.g., natal positions of 4° and 184° become 8° and 8° (368), 12° and 192° (552), 16° and 16° (736), and so on. If something is close but not exactly opposite, the behavior will be similar, but the positions will gradually separate.
I have tried to describe the antics of harmonics so some purely mathematical aspect of their behavior won’t be taken to be of great astrological significance. (“Look, his Sun is backing up!”, etc.)
That, then, is some of what is being done in the field of harmonics in astrology. With the techniques described, one can create a whole new set of charts to play with. However, that can use up a lot of time which can be better spent so I suggest that you let a computer do as much of the math as possible. Astro Computing Services, which has just moved from Pelham, NY to San Diego, CA, offers several harmonic services. They offer a harmonic sort of planets and midpoints for any integer divisor of the circle for $1.00. Positions are printed out with proportional spacing to make clumping easier to see. They offer a listing of positions for any 30 consecutive harmonics for $1.00. They offer any single harmonic chart in their great wheel for $1.00. They have a $1.00 per order handling charge. Their new address is Astro Computing Services; PO Box 16297; San Diego, CA 92116. They don’t currently offer anything for non-integers because that is very new and experimental.
Have fun exploring this new area!