Planetary Mandalas
Mark Pottenger
Inspired by Neil F. Michelsen’s book which came out in the summer of 1990 (Tables of Planetary Phenomena from ACS Publications in San Diego, CA), I moved the idea of creating planetary mandalas forward from the back burner. I actually started writing a planetary mandala program the evening of November 6, 1990. I have spent (and am still spending) quite a bit of time adding options and playing with it since. Below is a sample, and more will be elsewhere in The Mutable Dilemma and in Asteroid-World.
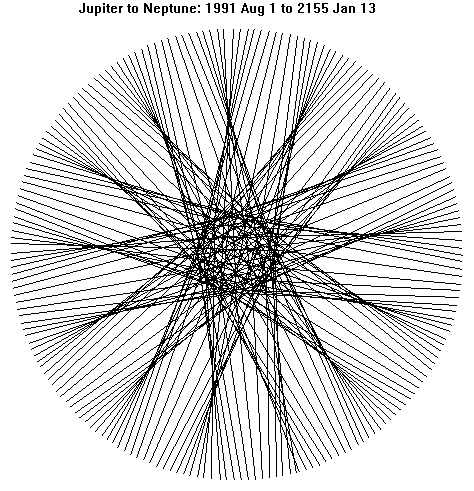
Planetary mandalas are a way of enjoying patterns. The technique I have used most draws straight lines between the positions on a solar system map of a pair of planets on a series of evenly spaced dates. Think of it as the diagram someone would produce by setting a timer and drawing a line between the current map placements of two planets whenever the timer goes off. The diagrams use standard (heliocentric) astronomical coordinates in the plane of the ecliptic. From this simple principle, a large variety of striking mandalas appear. The mandalas depend on the pair of planets chosen, the time between measurements, and the number of measurements. The time between the first measurement and the last can be anywhere from a few days to several millennia. (When the mandala incorporates millennia of motion, precession is a significant factor.) The basic motions being shown are circular or elliptical. The circles or ellipses or partial arcs of the two planets’ orbits can usually be seen, but sometimes they are not both obvious and sometimes other circles are more visible. Many mandalas include star patterns with varying numbers of points, and several sorts of heart shapes also show up. Some mandalas are quite simple and straightforward, but many contain enough ambiguity or complexity to allow viewers freedom to interpret them like Rorschach inkblots. Others can contain interesting features in both figure (lines) and ground (spaces).
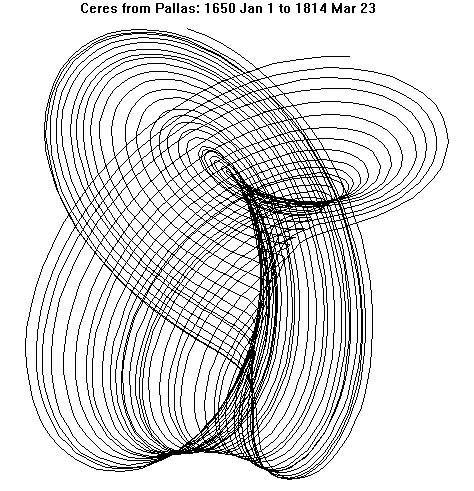
Another type of mandala maps the apparent position of one planet as it would be seen in a coordinate system centered on another planet. Most such figures look fairly similar, with circles and retrograde loops. A few are more intriguing: Ceres and Pallas stay no farther apart than a semisextile for many years, producing a fascinating map.
Beyond their visual appeal, I think properly chosen sets of mandalas can also be used as teaching tools to help illustrate points about planetary motion. Concepts like sidereal period (time to orbit around the sun), synodic period (time for two planets to return to a particular phase angle), the mutuality of retrogrades, the difference between heliocentric and geocentric returns, precession (movement of the coordinate system against a fixed backdrop) and more can all be illustrated.
Star points, horns, hooks, spikes, flares and hearts all come from changes in relative motion at various distances and phase angles. Many shapes come from harmonic relationships between the orbits of the planets (ratios between their orbital periods). The sampling interval (days between lines or points) can have a major effect on the final shapes produced. Short sampling intervals (a few days or even tens of days for outer planets) tend to produce fairly complete pictures of the overall relationship between the pair of planets chosen for the period shown, though sometimes the time period can make a significant difference. Longer sampling intervals can produce a variety of shapes not otherwise seen. Exact harmonic divisions and multiples of both sidereal periods and synodic periods can produce interesting mandalas. Exact sidereal periods have one end of all lines going to the same point—giving either a conical effect with the longer sidereal period or a rising sun effect with the shorter sidereal period. Exact synodic periods produce mandalas in which each line represents the same heliocentric aspect (as nearly as the circularity of each orbit involved allows), with the aspect you get determined by your starting date. Intervals slightly shorter or longer than the exact multiples produce whole new sets of shapes. Almost any combination of planets, dates and intervals might produce an informative or visually interesting pattern. Since my program lets me view the mandalas on screen as I create them, I only save and print the ones I find interesting for technical or visual reasons.
There are so many possibilities that verbal descriptions just can’t do justice to the subject. We will include mandalas on any partially blank pages in this and future issues of The Mutable Dilemma to let you, our readers, see for yourselves.