Primary Directions Follow-up
Mark Pottenger
In our Gemini 1987 issue we had an article about primary directions by Rique. I am now presenting a follow-up, since it was requested. Rique did the hard work, determining the correct trigonometry to find out when two points are on the same proportionate horizon. What I will discuss here is how you use that to get a full set of primary direction aspects and dates.
First, a correction: On page 3 in the Gemini issue, we had a typo defining the Ascendant as the intersection of the Equator with the Horizon. The correct definition is that the Ascendant is the intersection of the Ecliptic with the Horizon (in the east). Figure 3 on page 10 was drawn to match the text, and is also incorrect. A corrected figure 3 appears below.
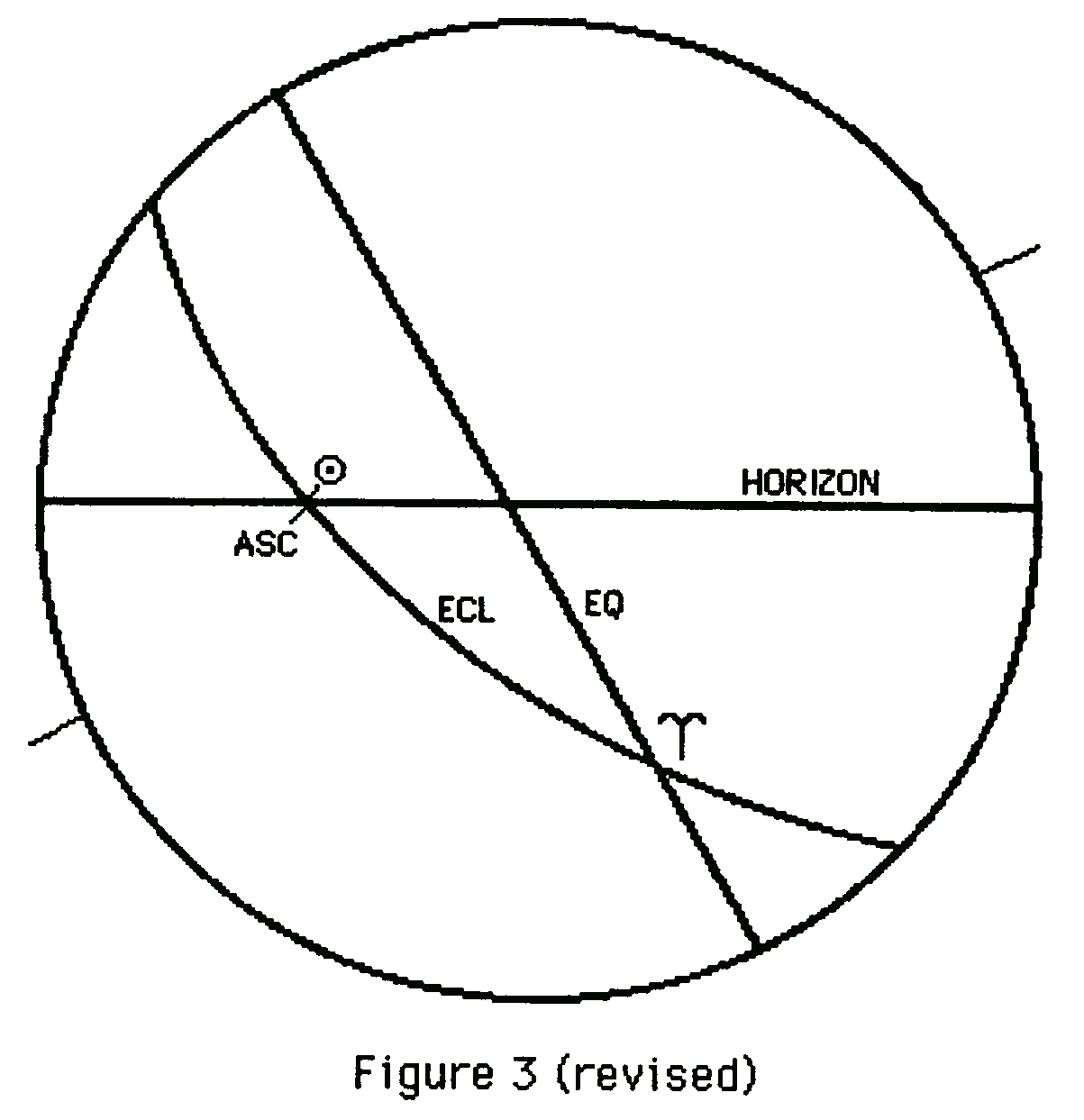
Rique showed how you calculate a planet’s pole, and then from the pole get the little ascensional difference, Q: Q = arcsine(tan(declination) x tan(pole)). From Q and Right Ascension, you get the planet’s Horizontal Ascension: HA = RA - Q. Two planets are considered conjunct in primaries when they have the same Horizontal Ascension.
If two planets don’t have the same Horizontal Ascension, the difference between their ascensions is the amount the earth would have to turn for one to reach the proportionate horizon of the other. This arc of direction is your basis for timing in primaries. (The natal positions are fixed, and the directed planets move past the natal positions.)
The first step in doing a full set of primaries is to convert all other aspects to conjunctions. You add the degrees in each aspect to a planet’s longitude to get the longitude of the ecliptic aspect point. You then do the rest of your calculations for the aspect point instead of the planet. (For example, to get a square to a planet at an absolute longitude of 30, or 0 Taurus, add 90 degrees to find that you will do your calculations with a longitude of 120, or 0 Leo. The other square is at 300, or 0 Aquarius.)
At this point, we get our first complication. Primaries work with Ascension. The first Ascension we get is Right Ascension (and its matching coordinate, declination), which we calculate from the zodiacal longitude and latitude of the planet. When we are working with a planet there is no ambiguity about this conversion, but when we are working with an aspect point we suddenly get arguments about what latitude to use! The definition of an aspect point above says nothing about latitude. The three choices used in primaries are: latitude of the natal planet, latitude of the directed planet, and zero latitude. Which choice you make can make a large difference in the Right Ascension and declination, and all following results. A complete primaries program will either show the results for all three latitude options, or offer you your choice.
An example of the effect of latitude: assume that the point at 0 Taurus mentioned above has a latitude of 2 south, and is being directed to the +90 square to a point with a latitude of 5 north. The three possible positions of the aspect point are:
|
Long |
Lat |
RA |
Dec |
|
120 |
-2 |
121.74 |
18.20 |
|
120 |
0 |
122.18 |
20.16 |
|
120 |
5 |
123.35 |
25.04 |
(Latitudes can get even higher than those shown here, making an even bigger difference.)
The second complication (or choice) in primaries is whether to use direct or converse directions. Direct primaries use the aspect point from the directed planet and the pole of the natal planet, measuring the arc required for the directed planet’s aspect point to reach the proportionate horizon of the natal planet. (Direct arc = directed planet’s aspect point’s Horizontal Ascension under natal planet’s pole - natal planet’s Horizontal Ascension.) Converse primaries use the aspect point from the natal planet and the pole of the directed planet, measuring the arc required to move the directed planet’s proportionate horizon to the aspect point from the natal planet. (Converse arc = directed planet’s Horizontal Ascension - natal planet’s aspect point’s Horizontal Ascension under directed planet’s pole.)
For example, a directed Horizontal Ascension of 60 minus a natal Horizontal Ascension of 20 gives an arc of 40, meaning the earth (sky) would have to turn 40 degrees to bring the directed planet to the natal planet’s proportionate horizon.
Note: because of the nature of the formula Rique described, you must use the pole of the planet whose proportionate horizon is being used for your calculations. Both natal and directed planet (or aspect point) Horizontal Ascensions are calculated using the same pole to get answers that can be compared. If you used the natal pole for the natal planet and the directed pole for the directed planet, you would be trying to compare two different proportionate horizons. This is why the Horizontal Ascensions above say “under the pole of” either the natal or the directed planet.
A confusion to avoid: Ascension, like zodiacal longitude, increases in a counterclockwise direction. Diurnal motion, which is the basis of primaries, is clockwise. This means that motion is in the direction of smaller numbers, not larger. Watch out for this if you see what looks like the wrong position being subtracted in a formula.
Once you have an arc of direction, you face another choice in converting that into dates in the life. There are four systems I am aware of (and have in the CCRS Horoscope Program): one degree per year, mean solar arc, birthday solar arc, and solar arc. Because the motion we are measuring is earth’s diurnal motion (a difference in ascensions), all of the timing systems use Right Ascension (measured along the equator) instead of the more common astrological use of zodiacal longitude (measured along the ecliptic).
One degree per year timing is obvious.
Mean solar arc (Naibod’s measure) divides each arc by 0.9856 to get years from birth. One degree of motion covers about 370 days.
Birthday solar arc divides each arc by the Sun’s motion on the day of birth (or for the 24 hours after birth) to get years from birth.
Solar arc is actually the same solar arc you would use in secondary (day-for-a-year) progressions, except for being measured in RA. The arc of direction matches the (RA) solar arc some number of days after birth, and that number of days gives you years of life for a final date.
These four techniques can convert arcs to dates in the life differing by years for people with an especially fast or slow sun.
Note: in a computer program, it is easier to work with days than with years for getting a date as a final answer. I do this by multiplying each arc by the length of a tropical year (365.242 days) along with the rest of the calculations. Some programmers might use a Julian year (365.25 days), but I prefer tropical.
The earth (sky) rotates 90 degrees in 6 hours, so all of the primary directions for an average lifespan represent motion in less than six hours. Primaries are very sensitive to the accuracy of the planetary positions used. Since one degree of motion covers a year of life (exactly in degree for a year, approximately in the solar arc timings), an error of one minute of arc in a planet’s position will produce an error of six days in the final answer.
We have mentioned that we think primary directions fell into disuse because they are so much work. Beyond all the procedures already described, there is one more factor that contributes to the difficulty of doing primaries. In most forms of progressions, directions and transits, you can just look at an ephemeris and know which planets will be forming which kinds of aspects. In primaries, you have to go through the full set of calculations for each aspect for each planetary pair to find out if the arc of direction falls within the period you are interested in. Whether I am getting 1 year, 5 years or 50 years of primaries, a program has to calculate all aspects for all planets and test after the fact to find which ones to print. Doing that by hand, you could do some pre-judging that particular aspects couldn’t fall in the period wanted, but you would still be faced with a huge amount of thrown-away work.
A distinction to remember: the techniques described here are for primary directions, not primary progressions as I occasionally hear people say. Directions take a set of positions at a specific moment in time and freeze them all with respect to each other and a celestial sphere. This set of positions (the whole celestial sphere) is then turned as a unit around some axis at a rate determined by the system being used. In the case of primary directions, we turn the celestial sphere to represent a part of a day’s motion. Progressions, on the other hand, use some ratio (day for a year, lunar month for a year, etc.) to determine that planetary positions at a particular time correspond to a specific date in the life. Progressions calculate new planetary positions for the time determined by the ratio, with all the usual variations in planetary motions. Progressions use positions that actually could have been observed in the sky, while directions create positions that were never in the sky. The technique described here is, by these definitions, a form of direction.
Even when you let a computer do all the math, you are faced with 24 choices of final results (3 latitude options x 4 timing options x 2 directions). I have no opinions about which options might be best. This is a question that has to be settled in the classical method of all astrology: try the different techniques and see what works.